Name: Разлом Rima Hadley. Американцы на Луне. Методика проверки фотоснимков Аполлонов
Item: Разлом Rima Hadley. Американцы на Луне. Методика проверки фотоснимков Аполлонов
Author: ligaspace

Длина не менее 135 км, шириной ~ 1,2 км и глубина ~ 370 м (от Грили (1971) указаны в Леверингтон Ф..

Интересное место посетили Аполлон 15. Есть снимки разлома со стереобазой. Вот они

До противоположного склона более 1 км, глубина 300 м. До изгиба разлом Хэдли 6 км. В натуре это выкопать невозможно в искусственной панораме. Значит противоположный склон должен быть "нарисован" или рядом в нескольких десятках метрах и на это укажет параллакс. Или же стереоскопический эффект покажет, что расстояния соответствуют лунным условиям. В этом случае надо признать, что стереоскопический эффект подтверждает пребывание американцев на Луне.

Речь пойдет о проверке расстояний на основе стереоскопического параллакса снимков Аполлон 15 вблизи разлома Хэдли.

Рис. 8. Топографическая карта Apollo 15 с большим разрешением. Зеленым указаны места съемки.

Метод проверки фотоматериалов лунных экспедиций Аполлон

Стереоскопический параллакс (от греч. parallaxis - отклонение) - видимое изменение относительных положений предметов на снимке вследствие перемещения фотокамеры. В библиотеке Аполлонов НАСА есть снимки с изображением одних и тех же объектов, которые выполнены при смещении камеры Хасселя по горизонту. Это значит, что можно проверить изображение на стереоскопический параллакс.

Из истории. Впервые данная методика была использована для лунных снимков в статье Новые исследования: Были ли американцы на Луне или нет? (30 января 2008 г.). Методика вызвала интерес и новые дискуссии между защитниками НАСА и оппонентами пребывания американцев на Луне. На данную методику и материалы ссылаются несколько сот источников, например, http://www.avanturist.org/forum/index.php?topic=682.320,http://www.forum.mista.ru/topic.php?id=462671&page=4.
За это время НАСА, с подачи Юрия Красильникова, в срочном порядке создало серии стереофотографий для красно-синих очков, анаглифы, накладывая пересекающиеся части снимков миссии Аполлон. Официальные представители НАСА их рекламируют в Глобальной Сети. Защитниками НАСА была написана некорректная ответная статья "Метод корреляционного вычисления параллакса и камуфляж", в которой сведение кадров производится в программе для создания круговых панорам PTGui, что стирает стереоскопический эффект предметов заднего плана. В Википедии "Лунный заговор" в конце 2009 года добавили: "Также анализ снимков лунной поверхности, сделанных во время экспедиции показывает, что удаление до предметов заднего плана действительно большое, что невозможно при комбинированных съемках в павильоне" со ссылкой на "Метод корреляционного вычисления параллакса".
Методика получила название "ligaspace метод параллакса".

Ниже приводится формализация данного метода с дополнениями.

Изображение на снимке создают точки, в цифровой технике – пиксели. Точки на снимке это x, y и z любого объекта и они являются неизвестными, буквально. Ибо по снимку можно только по визуальному ощущению говорить, что да, гора Хэдли удаленна на пять километров, до переднего края снимка 50 метров, до склона разлома Хэдли вроде бы 1 километр. И этим можно воспользоваться для фальсификации или создания коллажа. Однако, x, y и z любого объекта съемки можно определить, если у нас есть снимок с тем же ландшафтом, но со смещением камеры. Смещении камеры при съемке равнозначно смещению камней, кратеров, гор в случае лунных снимков, в общем смысле, равнозначно смещению ландшафта. Это значит, что каждой точке x, y и z одного снимка соответствует точка x, y и z на другом снимке. Положение такой точки на снимке определяется смещением камеры при съемке и оптикой камеры, или оптическим преобразованием:

смещение камеры – это три пространственных параметра X, Y и Z (более точно, плюс время - t), которые приводят к различию оптических осей, перспективным искажениям, масштабным изменениям, сдвигу, повороту одного изображения относительного другого.
оптика камеры – это дисторсия.

Теперь можно поставить задачу: определение расстояния z до объекта снимка по стереоскопическому параллаксу и решить задачу.
С точки зрения математики мы имеем систему уравнение, где каждая точка x, y и z любого объекта одного снимка выражена функцией от смещения и оптики камеры для точки x, y и z того же объекта другого снимка. Получаем систему нескольких миллионов уравнений, которую так же можно представить в виде расширенной матрицы Гаусса. Решение уравнений упрощается, если на снимках есть настолько удаленные объекты, что их параллакс равен нулю или близок к нулю. В этом случае точное знание оптики камеры опускается.

Систему миллионов уравнений можно записать одной строчкой:

P_i = (x,y,z)_1i - O(x,y,z)_2i ,

где P_i - значение стереоскопического параллакса; (x,y,z)_1i - точка i на снимке 1, соответствующая точке в пространстве x,y,z; O(x,y,z)_2i - функция оптических преобразований точки i на снимке 2, соответствующая точке в пространстве x,y,z; i - пробегает значение от 1 до полного значения числа пикселей.

Ясно, что если P_i = 0 (это точки удаленного ландшафта), тогда из системы уравнений определятся функция оптических преобразований. Далее, просто подставляем функцию оптических преобразований для точек в пространстве x,y,z, которые находятся на среднем или переднем плане снимка.

Конечно, знание оптики камеры значительно облегчает решение задачи. Например, знание дисторсии камеры позволяет быстрее произвести обратное преобразование для сведения снимков и получения стереоскопического эффекта. Но даже не зная дисторсию камеры, после решения задачи можно точно указать значение дисторсии.

Далее начинается решение миллиона уравнений методом графического вычитания пикселей снимков. Здесь под методом графического вычитания пикселей снимков подразумевается решение задачи путём преобразований изображения и представления данных вычитания изображений двух снимков. Проще говоря, делаем обратные преобразования снимка в следствии смещения и оптики камеры и смотрим вычитание точек снимков. При таком решении задачи помогают дополнительные условия, например, сохранение параллельности вертикали объектов на среднем и дальнем плане, другое.

Алгоритм выглядит так.

Снимки забрасываются в один файл программы работы с изображением, например, Фотошоп. Получаем два слоя изображений. Одному из слою изображения включаем функцию «разница» (вычитание или "difference”).
Первым преобразованием точек снимка является поворот снимка и смещение кадров относительно друг друга.
Вторым преобразованием является учет главных оптических осей и перспективы.
Третьим преобразованием является дисторсия и сдвиг.
Четвертое преобразование изменение масштаба снимка (если изучается масштабный стереоскопический эффект, тогда не используется).
Все преобразования выполняются так, чтобы получить максимальное вычитания между снимками (черный фон).

Это первое сведение одного снимка к другому или грубое решение задачи.

Далее начинаются многочисленные мелкие преобразования (поворот на доли градусов, перспектива, смещение на несколько пикселей, небольшая дисторсия, изменение масштаба на 0,5%…) одного снимка к другому.

Любое геометрическое преобразование снимка искажает оригинал.

Это известные программы редактирования изображения: (Аdobe Photoshop, Corel PHOTO-PAINT, Paint Shop Pro, Microsoft Picture It!, Visualizer Photo Studio, Pixel image editor, PixBuilder, Photo Editor, Fo2Pix ArtMaster и пр.. Мы ведем речь о первом.

Все геометрические преобразования в программе Аdobe Photoshop, как смещение, перспектива, дисторсия, масштабирование, поворот, сдвиг, сетка искажений - это трансформирование с числовым значением (ТЧЗ)

относительное смещение Х, Y в пикселях,
масштабирование по ширине и высоте в %,
наклон горизонтальный и вертикальный в угловых секундах,
поворот в в угловых секундах.

Любое одиночное трансформирование выполняется для точек изображения с субпиксельной погрешностью, не больше ±0,4 пикселя.

Для пяти последовательных трансформирований погрешности складываются для точки (пять раз накладывается ±0,4 пиксель) и составит не больше 2 пикселей, наиболее вероятная погрешность составит ±0,4 пикселя.
Для двадцати последовательных трансформирований погрешность составит не больше 8 пикселей, наиболее вероятная погрешность составит ±0,4 пикселя.
Для ста последовательных трансформирований погрешность составит не больше 40 пикселей, наиболее вероятная погрешность составит ±0,4 пикселя.

Официальные снимки Аполлонов, размещены на сайте НАСА, имеют два стандарта цифрового разрешения - 900х900 и 2300х2300. Для снимков с высоким разрешением относительная погрешность составит, соответственно,

для одиночного ТЧЗ ±0,0174%;
для 5 ТЧЗ максимальная 0,0869%, наиболее вероятная ±0,0174%;
для 20 ТЧЗ максимальная 0,3478%, наиболее вероятная ±0,0174%;
для 100 ТЧЗ максимальная 1,7391%, наиболее вероятная ±0,0174%.

В данном алгоритме грубое решение задачи (это пять геометрических преобразований)
приводит к погрешности обработки оригинала не более чем на 0,0869%. Точное решение (это до двадцати геометрических преобразований) приводит к погрешности обработки изображения не более чем на 0,3478%. Все указанные стереоскопические эффекты ближнего, среднего или дальнего плана имеют на порядки большие числовые значения.
Т.о. преобразования в программе Аdobe Photoshop сохраняет оригинал параллакса таким какой есть. И только при более чем стократном геометрическом преобразовании можно говорить о погрешности, которую вносит компьютерная программа обработки изображения.

Все преобразования рассматриваются и анализируются на основе данных вычитания изображений двух снимков.

В итоге мы получаем слой (изображения), у которого стереоскопический параллакс дальних объектов равен нулю (черный фон). Изображения переводим в нормальный вид и поочередно забрасываем в гиф-аниматор, получаем стереопару из двух кадров.

Пример таких стереопар:

стереопара, Змиевская электростанция, Украина

Рис. 9. Стереофотография Змиевской станции, Харьковская обл., 26 июля 2009 г. Скачать с высоким разрешением исходные снимки http://ligaspace.my1.ru/pic/IMG_21.jpg и http://ligaspace.my1.ru/pic/IMG_22.jpg

Рис. 10. Стереопара из двух снимков (http://i076.radikal.ru/1009/ac/6911358c9987.jpg и http://i053.radikal.ru/1009/37/dd95f1898993.jpg ) со стереоскопическим эффектом, позволяет определить расстояние до объектов. В данном случае до передних гор 2,5-3 км. Использованы оптические преобразования ко всему снимку: масштабирование, поворот, перспектива, дисторсия, дополнительно - сдвиг, а так же смещение по х и у...

Стерепара на основе снимков с глубокой перспективой

Рис. 11. Стереопара для снимков s002.radikal.ru/i197/1009/10/76b8cf38d3ae.jpg и s50.radikal.ru/i127/1009/1e/bae364969aaa.jpg после оптических преобразований с большим разрешением.

Надо отметить, что кроме горизонтального параллакса есть вертикальный, масштабный (связанный с приближением к объекту съемки) и смешанный параллаксы. Это связано со смещением камеры в пространстве по х, y и z координатам. Каждый из стереоскопических эффектов можно выделить по отдельности, как и изучать в целом, убрать все стереоэффекты и изучать динамику (например, меняется ли задний фон, чтобы сказать о его искусственной подстановке). В случае горизонтального или масштабного параллакса мы можем определить расстояние до объектов и указать погрешность.

Относительная погрешность измерения Errors будет выражаться отношением погрешности измерения (max - 2 пикселя для цифровой фотографии) к измеренному значению величины стереоскопического смещения X в пикселях, в процентах:

Errors = 200/X

Наконец, удаленный ландшафт на стереопаре можно изучать на симуляцию. Для этого выходят за рамки оптических преобразований и производят цифровое искажение по элементам, а не в целом к снимку, приводя их в точности друг к другу. Интересным объектом является результат преобразования или сетка искажений удаленных объектов на снимках. В рамках данного метода можно определить характер симуляции удаленного ландшафта. Это например, было сделано А. В. Крамаренко, Ю. А. Крамаренко, дальние объекты были сведены не оптическими преобразованиями. Так же Юрий Красильников в программе для сборки панорам Hugin, сводит снимки (10.07.2009).

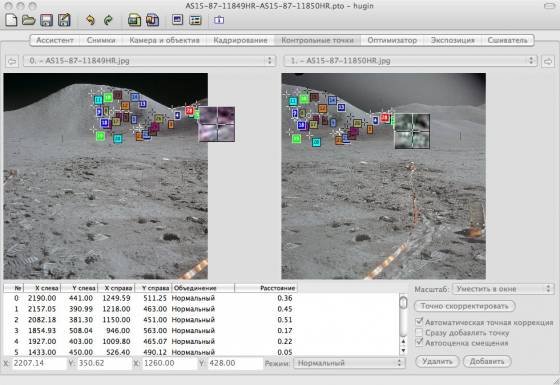
Сборка лунных снимков в стереопару

Рис. 12. Обработка изображений AS15-87-11849 и AS15-87-11850 в программе сборки панорам Hugin по Ю. Красильникову

К сожалению, данными авторами не была указана сетка искажений, исследования до конца не были проведены. Очевидно, что если сетка искажений имеет криволинейную поверхность, тогда она соответствует обратной проекции на плоскость круговой панорамы. Проще говоря, это симуляция удаленного ландшафта на киноэкран. Можно грубо оценить радиус круговой панорамы.

Таким образом, графическое сведение снимков в стереопару с требованием максимального вычитания удаленного ландшафта - задача не простая, требует аккуратности и времени. Ясно, что решение системы уравнений из более чем миллиона уравнений в рамках оптических преобразований, выход за эти рамки и получение сетки искажений вокруг места съемки намного весомое доказательство, чем просто идея.

Автор: Олейник О. Г.

Далее будет - ширина разлома Хэдли по снимкам Аполлон 15 составляет несколько десятков метров; сетка искажений для горизонта снимков указывает на симуляцию удаленного ландшафта или на киноэкран - Разлом Rima Hadley. Существует ли лунный заговор? Стереоскопический параллакс снимков.

Дополнительные материалы:

Automatic Translator

Rima Hadley. Americans on the moon. Methods of test photos Apollo