 Photographs taken on the
lunar surface during the Apollo missions are regarded as the most
compelling pieces of evidence that mankind went to the Moon. Photographs taken on the
lunar surface during the Apollo missions are regarded as the most
compelling pieces of evidence that mankind went to the Moon.
The photographic validation methodpresented
here is based on the detection of two-dimensional objects among
three-dimensional objects, and determining the mutual arrangement of
these objects in space and the distance to them by applying a technique
known as stereoscopic parallax.
The word parallax derives from the Greek parallaxis meaning "alteration"
where parallax is the difference in the apparent position of objects
caused by shifting camera position. To achieve such a result, images are
overlapped and are deducted/subtracted from each other using the
function "difference" in an image processing application such as
Photoshop®. Optical transformations are
used when images are subtracted. During image convergence simple
operations are applied: x and y axis scaling, rotation and distortion
plus two additional processes: perspective and shift.
Such processes are referred to below as "optical transformations".
Objects further than two kilometres distant, with a minor camera shift,
have zero parallax.
Using Photoshop® the sequence of steps deployed is as follows:
- Two overlapping images are placed on different layers – thereby creating a PSD file.
- Application of function "difference" to the upper layer (subtraction of images from each other).
- Optical transformations are applied: axes x and y scaling,
rotation, distortion, perspective and in addition a shift to the
requirement specified above. As a result maximum density black for the
background is obtained.
- The layer is returned to the normal view: function "normal".
- The PSD file is pruned to remove non-overlapping parts.
- Sequentially, the converted layers are carried over into the application’s GIF animator.
- A stereoscopic GIF image is obtained that permits the creation of a 3D effect, even on a flat screen.
 Fig. 1. A stereoscopic image or
‘wiggle’ stereoscopy. GIF-animation allows the creation of a crude sense
of dimensionality, even with monocular vision. Stereoscopic imagery can
also determine the relative position of objects in space and enable
judgment of their remoteness. Image Wikipedia Fig. 1. A stereoscopic image or
‘wiggle’ stereoscopy. GIF-animation allows the creation of a crude sense
of dimensionality, even with monocular vision. Stereoscopic imagery can
also determine the relative position of objects in space and enable
judgment of their remoteness. Image WikipediaIf any given image was taken inside a
pavilion or dome with a panoramic background, i.e. when there are no
distant objects with null parallax, then such a 2-dimensional object can
be detected among any 3D bodies. In the case of such a finding,
reaching the conclusion that there was deception could be stated with
confidence.
Example 1. The method of creating a
stereoscopic image is examined in the following example of images of the
Zmievskaya power plant, Kharkov region, Ukraine. The camera shift is
1.5 m. The distance to the power plant is about 4 kms and to the tree planting (left horizon) is about 2 kms.
The image convergence shown below (the main criteria is the most
complete background subtraction, and since the distance is more than 3
kms, the parallax is zero).  Fig. 3. Image subtraction. Fig. 3. Image subtraction. Images are processed in a GIF-animator to obtain a stereoscopic image:
 Fig. 4. Stereoscopic image of the Zmievskaya power plant. Fig. 4. Stereoscopic image of the Zmievskaya power plant. (For more detailed information on creating stereoscopic images and obtaining intermediate images see this article – in Russian). It is now possible to measure the parallax and the distance to all remote objects. The distance La to any object A, is calculated as follows: Knowing the distance
to the front edge: 5 m, and the front edge offset: 85 mm (can be
measured by a ruler, the two white grasses), plus the offset of the
nearest electric pylon, about 1.2 mm. From the proportions ratio the
distance to the nearer pylon is acquired, namely 350 metres; to the
second pylon with the parallax of 0.6 mm is 700 metres. Distance to the
trees (offset is about 0.2 mm) is close to 2 kms – at the boundary of
parallax occurrence. Conclusion: These simple image transformation operations preserve perspective proportions.
Similarly, as in the case of examining the parallax of the Apollo
lunar surface images – where, according to NASA maps of the landing
sites, the distance to the mountain background should be more than 5 kms
– evidence of stereoscopic imagery is expected. If such evidence is
absent, the image cannot have been taken in the stated environment, such a image must have been created elsewhere in a studio.
Having looked at stereoscopic parallax in images of
terrestrial objects, some Apollo images are studied from the
photographic record.
The Apollo 15 LM touched down at 22:16:29 UTC on July 30 1971 at
Hadley (26°7'55.99"N 3°38'1.90"E), near Hadley Rille (also referred to
as Rima Hadley), Montes Apenninus and Mons Hadley. The first lunar rover
was used for extensive reconnaissance. Within 67 hours the crew carried
out three EVAs, spending 18.5 hours in total away from the LM. A new
500mm lens, camera and accessories were used, which have provided
photographic opportunities not available to previous missions. Lift off
from the lunar surface was on August 2, 1971 and the astronauts returned
to Earth on August 7.
The Apollo 15 crew comprised:
- Commander David R. Scott (Dave)
- Command Module Pilot Alfred M. Worden
- Lunar Module Pilot James B. Irwin (Jim)
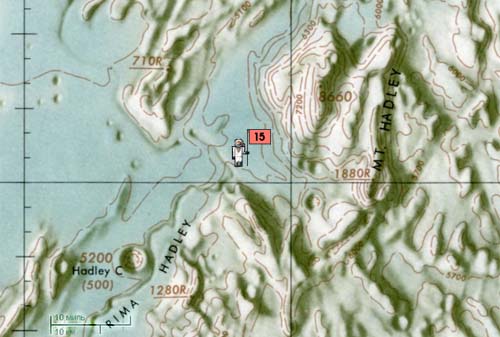 Fig. 5. Topographic map of the Apollo 15 landing site. Fig. 5. Topographic map of the Apollo 15 landing site.A series of Apollo 15 photographs will be
considered and stereoscopic parallax or apparent change in the relative
positions of objects will be analysed. The first series. Astronaut Dave takes a few panorama images in EVA-1 near the LM, AS15-86-11601 and AS15-86-11602.   Fig. 6. The LM with Jim standing
at the rear of the rover; the Apennine front and the crater St. George
are located in the background. The distance from the camera to the lunar
module and rover is about 10 metres, and the Apennines and the crater
should be 4-8 kms away. Fig. 6. The LM with Jim standing
at the rear of the rover; the Apennine front and the crater St. George
are located in the background. The distance from the camera to the lunar
module and rover is about 10 metres, and the Apennines and the crater
should be 4-8 kms away. A rectangle marks the sections of the photographs which were
deducted for parallax examination and separation of 3D objects from any
2D objects.
  Fig. 7. The subtraction of the
two photos after the transformations of scaling, rotation, and
distortion is shown on the left. The right image shows the parallax
achieved after merging the two frames. Fig. 7. The subtraction of the
two photos after the transformations of scaling, rotation, and
distortion is shown on the left. The right image shows the parallax
achieved after merging the two frames. Nearby objects: the LM, the rover, and astronaut Jim are
shifting relative to each other. The Apennines and the crater St. George
are also moving as a whole. (Moreover, the shadow is changing on the
mountains and the crater.) This finding indicates that it is less than 300 metres to the background (the ‘mountains’) instead of 5 kilometres! Therefore, with such a small alteration to the camera position
in Dave's hands (several tens of centimetres), the mountains should not
move, they should remain static (zero parallax). In addition, the Apollo 15 stereoscopic photos feature a clear
separation line between the ‘mountains’ and the foreground. Based on
the distance between the camera and rover, the distance to the panorama of the ‘lunar’ scape cannot be more than 150 metres. Conclusion: It is very probable that these images were taken on Earth in a studio stage. The second series. Jim is doing some panoramic photography (Fig. 8). The distance from his camera to the LM is approximately 40 m. Jim's ALSEP Pan at the end of EVA-2.
 Fig. 8. On the left Dave collects
samples; Mount Hadley; LM in the centre; behind the LM the sun is
shining into the camera and the Apennines are in the distance – over 35
kms; the Apennines and the crater St. George are on the right at a
distance of 5-8 kms. The two images with a view of Mount Hadley
were selected from the Panorama (distance is about 30 kms, the height
more than 2.5 kms) AS15-87-11849 and AS15-87-11850.   Fig. 9. Note the numerous boot prints left by Dave and Jim. Fig. 9. Note the numerous boot prints left by Dave and Jim. Rectangles highlight the selected areas selected for parallax examination.
  Fig. 10. The subtraction of two
images after scaling, rotation, and distortion is shown on the left. The
stereoscopic image after merging two images is on the right. Fig. 10. The subtraction of two
images after scaling, rotation, and distortion is shown on the left. The
stereoscopic image after merging two images is on the right. Despite a slight offset of the camera, the mountains are
moving, which contradicts the condition of distant mountains. If the
image subtraction criteria are changed, the most darkened background
condition is replaced with the most darkened front area.
  Fig. 11. The subtraction of the
front parts of the two images is on the left. The parallax resulting
from the two merged images is on the right. This image was obtained by
the subtraction of two photos taken with a camera shift of not more than
20 cms. Transformations of scale, rotation, reverse distortion,
perspective, shift and the convergence of the two images into a
stereoscopic image were applied. Fig. 11. The subtraction of the
front parts of the two images is on the left. The parallax resulting
from the two merged images is on the right. This image was obtained by
the subtraction of two photos taken with a camera shift of not more than
20 cms. Transformations of scale, rotation, reverse distortion,
perspective, shift and the convergence of the two images into a
stereoscopic image were applied. An error estimate is now performed. Assuming that this is a
real lunarscape, then the distance from the astronauts to the lunar
horizon should be 1.5 kms and the distance to the objects in the
background, such as the foot and summit of Mount Hadley, is 20-35 kms. The offset of 100 sampled pixels below the horizon is
calculated – the AB line, obtaining an average shift ± a pixels
(depending on the image resolution). The shift magnitude obeys Gaussian
distribution, meaning this is noise. A sample of 50 points is selected above the line (AB), i.e.
objects located at a distance of 20-35 kms. Giving an offset value of
(10-50)a pixels. The shift direction has a vector and is not subject to
Gaussian distribution. Moreover, the higher a dot the greater value of
the shift – at the foot it is 10a, at the top 50a pixels. It is logical to assume that if any lunar objects at the
interval [0.01; 1.5] kms are static, the noise amounts to ± a, the
parallax is zero, then for more distant objects at the interval [20; 35]
kms, the parallax is likewise zero with the same value of noise, i.e.
the shift is ± a pixels and the shift value obeys a Gaussian
distribution. However, the results indicate otherwise. Objects above the (AB) line are moving synchronously with increase in shift depending on the height above the horizon. Conclusion: Mount Hadley moves and
‘bows’. The wrong initial assumption was probably made that this is a
real lunarscape. As this research demonstrates, this setting must be a totally artificial panorama, several tens of metres in depth with a mock ‘Hadley’ in the background, moving horizontally and vertically to create an illusionof remoteness and of perspective. A series of Apollo 15 images are now examined near Rima Hadley
for the presence of stereoscopic parallax. Rima Hadley measures in
length at least 135 kms, with an average width ~1.2 and average depth
~370 m (from Greeley 1971 – quoted in F. Leverington, 2008). The third series. Dave and Jim make a
few trips in the rover to Rima Hadley (Fig. 12) to collect samples. One
of the panoramas comprises photos from AS15-82-11165 to AS15-84-11284.  Fig. 12. Jim is holding the
camera. Rima Hadley is in the foreground. Dave is collecting samples
near the rover. Mount Hadley is in the background. The sun is shining
into the camera in the centre. The Apennines are over 35 kms away.
Apennines Front and the crater St. George are on the left.
(Panorama assembled by the author)
In two panorama frames is the bottom of Rima Hadley, which
extends to Apennines Front and the crater St. George. The distance from
the camera to Rima edge is about 5 m, to the Apennines and the crater is
4-8 kms. The frames are taken with a shift of no more than a few tens
of centimetres. AS15-82-11178 and AS15-82-11179.
  Fig. 13. The view of Rima Hadley, Apennines Front and the crater St. George. Fig. 13. The view of Rima Hadley, Apennines Front and the crater St. George.
Rectangles mark the sections used for parallax examination.  Fig. 14. The foreground
subtraction of the two images after scaling, rotation, distortion, shift
and perspective is on the left. On the right is the resulting parallax
obtained after merging the two frames. Fig. 14. The foreground
subtraction of the two images after scaling, rotation, distortion, shift
and perspective is on the left. On the right is the resulting parallax
obtained after merging the two frames.It is possible to see the movement of the
surface areas relative to each other along the edge of the trench
between points A and B. This situation cannot occur in real world photography.
Conclusion:These images were probably taken on Earth
in a dome-shaped studio location where movable panorama backgrounds
were installed, and even treated afterwards by further adjustment in a
photographic lab.
Fig. 15. Landscape and Traverse map of Apollo 15 landing site by NASA artist (showing stations 1-14). Images AS15-85-11423 and AS15-85-11424 were selected, taken at station 2 with Rima Hadley observation.
Fig. 16. Images AS15-85-11423
and AS15-85-11424 station 2 with a view of Rima Hadley. Photo camera
stereobase is not more than 0.5m.
The topophotomap (Fig. 17) shows that the opposite slope is
over 1 km away, the depth is 300 metres, and it is 7 kms to Rima Hadley
bow. It is impossible to excavate an artificial canyon of similar size.
Therefore, if fakery was involved, the opposite slope would have to be
‘painted’ or have a length of several tens of metres, simulating a lunar
landscape. On the other hand, if the photographs are genuine, the
parallax analysis will show that the distances correspond to the actual
lunar surroundings, confirming the NASA record.
Horizontal stereoscopic effect
For this parallax we apply the next set of transformations: optical zoom, rotation, distortion, perspective, shift in x and y
directions to the image as a whole. The requirement of maximum
deduction of remote landscapes is imposed to extract horizontal
stereoscopic effect.
As a result, we obtain the following stereoscopic pair of images:
Fig. 18. A stereoscopic pair of
images AS15-85-11423 and AS15-85-1142 with horizontal stereoscopic
effect after applying image transformations. Stereoscopic parallax is clearly visible in
Fig 18, and we can make a preliminary estimation of the distance to the
opposite slope of Rima Hadley. The distance is 50 metres
(recall that it should be at least 1 km according to the map). The
distant background is shifting slightly, although the parallax must be
zero, since according to the map it is about 20 kms to the mountains.
In general, given that in the true lunar background remote
objects should be located many kms away, it is impossible to achieve a
zero stereoscopic parallax using only previously-mentioned image
transformations – confirmed by converging dozens of pairs of Apollo
lunar surface images (as well as numerous efforts by other researchers).
This strongly suggests that the distance to remote objects in the
Apollo photographs which should be many miles/kms is indeed not so. These images are a simulation of being on the Moon.
How were these fake Apollo lunar surface images taken? Due to
incomplete convergence of remote background imagery a parallax error at
the foreground of stereoscopic images is revealed. The relative error
is a ratio of the foreground object’s shift in relation to the
background object’s shift.
Distortion grid of background lunarscape
The remote terrain in a stereoscopic pair of images can
be converged precisely with each other. To do so it is necessary to go
beyond the optical transformations applied to the image as a whole and
introduce digital distortion to the sections of the image.
This method can determine the nature of simulation of any
background 'land'scape i.e. build a distortion grid and inspect it.
Obviously, if the distortion grid has a curved surface, then it
corresponds to projection at the rear onto a circular panorama screen,
creating a simulation of a remote background scape on the projection screen. Instead
of taking pictures in a remote lunarscape the ‘astronauts’ take
pictures of a foreground with the background projected onto a screen.
The radius of the circular panorama can be roughly estimated by a distortion grid.
Fig. 19 below shows the distortion grid. A million pixels were
involved in the transformation of these two images. In mathematical
terms this is a system of a million equations solved with sub pixel
accuracy.
 Fig. 19. Digital distortion
grid of background objects in AS15-85-11423 after optical
transformations converging with AS15-85-11424. A precise, curved concave transformation applied to the megabit pixels image confirms the fact that a ‘lunar’ scape was projected onto a forward-tilted, slightly convex panorama background screen. Any other technique fails to replicate the nature of the remote 'land'scape simultaneously for a million pixels of the image. 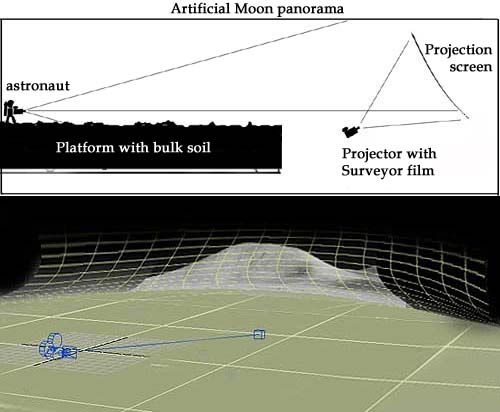 Fig. 20. Illustrates the logic and simplicity of a simulated Apollo lunar surface panorama. Fig. 20. Illustrates the logic and simplicity of a simulated Apollo lunar surface panorama.
The grid represents the projection screen which surrounded the Apollo simulation studio. Below is the final result of the transformation (optical
transformations and the circular panorama are already taken into
account).
Fig. 21. Rima Hadley view. Apollo
15 stereoscopic photographs AS15-85-11423 and AS15-85-11424 after image
transformation and digital non-linear distortion of the distant
landscape.
Distances to the image elements are specified in metres with an accuracy of 1%, 2%, 15%, 30%
and 45% of distances 3, 11, 20, 40 and 60 metres respectively. According to the map
the distance to the opposite slope of Rima Hadley should be about 1,000-1,200 metres. The parallax of the distant background is zero. In Fig. 21 we can see that the distance to the opposite slope of Rima Hadley is only 40 metres, while according to NASA's map it should be nearer to 1,000-1,200 metres. The difference is more than one of magnitude! This finding is seriously at odds with the official Apollo 15 record.
Scale stereoscopic effect
A scale stereoscopic effect was considered for AS15-85-11423 and AS15-85-11424 along the z
axis. For example a photographer takes a photograph in one position,
then moves closer to, or further from the subject and takes another
photograph.
Fig. 22. A stereoscopic pair of
images AS15-85-11423 and AS15-85-11424 with scale stereoscopic effect
after transformations: 1) applying transformations: scaling, rotation,
distortion, perspective, shift, and offset in x and y to the image as a
whole; 2) digital distortion of the distant background terrain; 3)
maximum subtraction of a distant background terrain, and 4) acquisition
of scale stereoscopic effect. Distances to the image features in metres
are specified with 60% accuracy. Scale stereoscopic parallax is clearly
visible in Fig. 22, which is used to estimate the distance to the
opposite slope of Rima Hadley. The distance is about 40 metres. The scale stereoscopic effect also points to fakery of the genuine Rima Hadley on the Moon.
Verifying the universal nature of a distortion grid
for a distant background scape
To verify the possible presence of a circular panorama
background screen, another pair of Apollo 15 lunar surface images
AS15-85-11424 and AS15-85-11449 with a view of the Rima Hadley taken at
station 2 are examined.
 Fig. 23. AS15-85-11424 and AS15-85-11449 with a view of Rima Hadley taken at station 2. Fig. 23. AS15-85-11424 and AS15-85-11449 with a view of Rima Hadley taken at station 2. Below is a digital distortion grid on the distant background
landscape present in images AS15-85-11424 and AS15-85-11449. A
million pixels of the two images are converged with sub pixel accuracy.
Fig. 24. Distortion grid of the distant background 'land'scape in AS15-85-11424 and AS15-85-11449. This confirms the previous finding that the ‘lunar’
mountain backscape was projected onto a forward-tilted, slightly
convex, circular panorama background screen.
Horizontal stereoscopic effect
By the following procedures of:
- applying optical transformations such as scaling, rotation, distortion, perspective, shift and
offset in x and y to the image as a whole;
- taking into account presence of a circular panorama;
- satisfying the requirement of maximum subtraction of a distant landscape;
- extraction of horizontal stereoscopic effect, we obtain the following stereoscopic pair:

Fig. 25. A stereoscopic
pair of AS15-85-11424 and AS15-85-11449; view of Rima Hadley after
transformations and digital distortion of the distant background
backscape. Distances to the features of the picture are specified in
metres with errors of 15%, 45% and 95% for distances 20, 45 and 140 m
respectively. According to the map the distance to the opposite slope
of Rima Hadley is approximately 1,000-1,200 metres; to Rima Hadley bow
is about 7 kms. From previous calculations the distance is
known to the foreground rocks at the bottom of Rima Hadley. Based on
parallax it is possible to estimate the distances to the other objects
as indicated in Fig. 25. Obviously errors are accumulative, the sum of
any distance errors to the foreground rocks at the bottom of Rima
Hadley as well as any errors in determining the shift of other features
of the image – in this case 15%.
Scale stereoscopic effect
A scale stereoscopic effect was also obtained for AS15-85-11424 and AS15-85-11449 along the z axis when the camera was moved nearer to the object.
Fig. 26. A stereopair of images
AS15-85-11424 and AS15-85-11449 with scale stereoscopic effect after
transformations of: 1) scaling, rotation, distortion, perspective shift
and offset in x and y to the image as a whole; 2) maximum subtraction of
the remote landscape; 3) obtaining a scale stereoscopic effect.
Specified distance to the elements of image in metres with an error not
more than 85%.
The scale stereoscopic parallax is clearly visible in Fig.
26. Using distances determined from the scale parallax, the distance can
be estimated to the opposite slope and to Rima Hadley bow. The distance
to the opposite slope of Rima Hadley is no more than 40 metres, and the
distance to the Rima Hadley bow does not exceed 140 metres.
According to the topographic map, distances to these locations
are more than 1 km to the slope and to Rima Hadley bow it is about 7
kms. Here again, there are serious anomalies in this Apollo record.
From a scale stereoscopic effect it is possible to estimate the distance
to Rima Hadley bow and to the background projection screen.
Fig. 27. A stereopair of images
AS15-85-11424 and AS15-85-11449 with a scale stereoscopic effect after
transformations and application of the distortion grid
for a distant landscape. The relative error in distances is no more than 60%. Based on the stereoscopic result, the calculated distance to
the mountains on the horizon is 140 metres (accuracy 60%). According to
the map it should be more than 20 kms. The difference in distance is
more than 100 times! These serious errors in the Apollo 15 photographic
record indicate that these images were undoubtedly faked.
The study of stereoscopic effect in photographs AS15-85-11423, AS15-85-11424 and AS15-85-11449 shows that these images do not contain distant objects farther than a few hundred metres away. The
distance to the opposite slope of "Rima Hadley" is about 40 metres
(should be 1,000-1,200 metres), to Rima Hadley bow is about 90 metres
(based on the topographic map is about 7 kms) and to the mountains it is
100-140 metres (should be nearer to 20 kms based on the lunar
geography). The error in calculation of these distances is 15-60%.
Contradictions in the photographic record of the Apollo
program point to the simulated nature of the lunarscape: creation of an artificial canyon,
40 metres wide and 90 metres long, simulating Rima Hadley with help of a
rear background screen, depicting a distant lunarscape.
Was there a way to simulate the remote lunar surface on a
projection screen for any other Apollo 15 lunar surface photographs?
More Apollo 15 images are considered from the NASA record with distant
lunarscapes.
In Fig. 7 after optical transformations, all the foreground
objects: the LM, the rover, and astronaut Jim move relative to each
other. Any distant object such as the Apennines and the crater St.
George also move as a whole. Shadows on the mountains and on the crater
change as well. The separation line between the mountain and the foreground area is clearly visible.
A rough estimate of the stereoscopic effect gives the distance to the
background (mountains) as less than 300 metres. Instead of the 5 kms
according to the Apollo record.
To converge a remote lunarscape a distortion grid was
superimposed onto the optically-transformed images AS15-86-11601 and
AS15-86-11602.
 Fig. 28. A distortion grid of the distant backscape for the converged images
AS15- 86-11601 and AS15- 86-11602 in the stereopair. Fig. 28 shows the distortion grid for
converging AS15-86-11601 and AS15-86-11602 to obtain zero stereoscopic
parallax. Recall that introducing a distortion grid is the method of
going beyond the standard optical transformation – the system of
creating equations for a one-million pixel image. Going beyond the laws
of optics in converging two pictures into a stereopair questions the
veracity of the image and results in a postulation that the lunarscape
was faked.
The regular curved repetitive distortion grid for other pairs
of images indicates projection of the distant background mountains onto a
rear screen positioned about 100 metres away with the ‘astronauts’ in
the foreground.
After applying the distortion grid we obtain the following stereopair:  Fig. 29. Stereo image after
combining two pictures AS15-86-11601 and AS15-86-11 602 for parallax
study. Line AB is a horizon mark at the foot of the mountain, above
which is a projection on the screen to simulate a lunar mountainscape.
The contrast was increased and the brightness was reduced. The familiar distortion grid was superimposed
on to the "distant" 'land'scape in photographs AS15-87-11849 and
AS15-87-11 850, and after optical transformation: Fig. 30. A distortion grid of the distant 'land'scape for converging two photographs
AS15-87-11849 and AS15-87-11850 into a stereopair. Fig. 30 shows the distortion grid of the distant background
in images AS15-87-11849 and AS15-87-11850. Taking this distortion grid
into account, a stereopair is obtained:
Fig. 31. A stereopair of two
images AS15-87-11849 and AS15-87-11850 to study the dynamics of the
scene after application of optical transformations and imposing the
distortion grid. Fig. 31 shows a stereopair of images
AS15-87-11849 and AS15-87-11850 to study the dynamics of the lunarscape
after application of optical transformations and imposing the distortion
grid. Obviously the distortion grid is a method of going beyond optical
alterations and is an indicator of simulation of the lunarscape and the
lack of really distant objects that should be several kilometres away.
The nature of simulation for a given pair of images is similar to the
previous pairs of images. Fig. 32. A stereopair based on AS15-82-11178 and AS15- 82-11179, after scaling,
rotation, distortion, shift and perspective.
Fig. 32 shows a stereopair of images AS15-82-11178 and
AS15-82-11179, which is obtained based solely on optical
transformations. A distortion grid is superimposed on the remote
lunarscape of one of the stereo photos AS15-82-11178 and AS15-82-11179,
and obtain:
 Fig. 33. A distortion grid of the remote 'land'scape for converging photographs Fig. 33. A distortion grid of the remote 'land'scape for converging photographs
AS15-82-11178 and AS15-82-11179. Another pair of photographs taken at the station 9-11,
AS15-82-11121 and AS15-82-11122 points up the fact that the image of the
mountain and central part of the Rima Hadley was projected onto a
background screen. Below is the final stereopair after optical
transformations were applied and imposing the same distortion grid on
the remote lunarscape as previously.
 Fig. 34. A stereopair
AS15-82-11121 and AS15-82-11122 after optical transformations and
overlaying a distortion grid on the remote landscape. Official distance
to the slope of Rima is indicated as being not less than 1,500 metres
and the value based on parallax – Fig. 34. A stereopair
AS15-82-11121 and AS15-82-11122 after optical transformations and
overlaying a distortion grid on the remote landscape. Official distance
to the slope of Rima is indicated as being not less than 1,500 metres
and the value based on parallax –
50 metres (error not more than 60%). The distance to the opposite slope of the Rima Hadley is 50
metres. The foot of the mountain and the Apennines can be clearly seen. Undoubtedly, this is a projected image on to a screen
taken by ‘astronauts’ (AS15-82-11121 and AS15-82-11122). The actual
length of the Rima Hadley on the Moon is actually 135 kms, the width is
about 1.2 kms, and the depth ~370 metres.
Study Conclusion
Professor of University of California G. Schiller has
noted: "To be successful, manipulation should remain invisible. The
success of the manipulation is guaranteed when the manipulated believe
that everything happens naturally and inevitably. In short, manipulation
requires a false reality in which its presence will not be felt". Very
often this false reality is amplified by the media.
In the convergence of these Apollo 15 pictures, more than a
million equations (the number of pixels in the images) were calculated
obeying the laws of optics. In order to obtain a zero stereoscopic
effect for a remote landscape, typical distortion grids were generated
around the photographic session sites.
Numerous Apollo 15 photo examples indicate an identical distortion grid – a projection screen at the distance of 100-120 metres from the front of the studio stage.
A serious falsification of the true lunarscape, in particular, an
artificial trench 30-60 metres in width given for the lunar Rima Hadley
which is actually 1,200 metres in width; the image of this remote
lunarscape being projected onto the curved background screen; and
‘astronaut’ photographers taking pictures in front of it in a studio
set.
The Apollo 15 photographic record contradicts the stereoscopic
parallax verification method. The apparent change in the relative
positions of objects by moving the camera when the camera angles are
separated by several tens of cms show that:
- the distance to distant objects such as mountains is not tens of kilometres but is no more
than a few hundred metres;
- the landscape is not continuous, but with clear lines of separation;
- there is movement between nearby sections of the panorama relative to other sections.
Thus, based on the above examples, this study
concludes that the Apollo 15 photographic record does NOT depict real
lunarscapes with distant backgrounds located more than a kilometre away
from the camera. These pictures were, without doubt, taken in a studio set
– up to 300 metres in size. A complex panorama mimicking the lunarscape
shows degrees of movement, such as horizontal and vertical changes to
give an impression of imaginary distance to the objects and perspective. Dr Oleg Oleynik
English translation from the Russian by BigPhil Aulis Online, April 2012
Afterword
Two years have passed since the
original publication of this article in Russia. During that time, NASA
decided to create a series of stereo photographs for 3D red-cyan glasses
(anaglyph images), superimposing overlapping parts of Apollo surface
photos. Reports slip out now and then that some of the photos on NASA’s
Web sites have been replaced by retouched counterparts.
An article entitled "The method of correlative calculation of parallax and camouflage" was
published (in Russian). I criticized the article stating that: "The
merging of frames is carried out in the application for creating 360
degrees panoramas PTGui, which erases parallax, and eventually the distance to background objects artificially increases. Please double check the algorithm of the application". More here (In Russian).
There was no answer from NASA. Instead, in the Russian Wikipedia, late
2009, the following paragraph was added (and removed on July 31, 2011)
to The Moon Hoaxarticle:
"Also, analysis of the lunar surface images, taken during the missions
shows that distance to background objects is indeed vast and cannot be
achieved in a soundstage with trick photography", referring to "The
method of correlative calculation of parallax and camouflage"
publication. Any attempts to change or
correct the information in Wikipedia, and to point out the serious
errors in the Wikipedia article did not succeed, the moderator continued
to erase the link.
Dr Oleg Oleynik
About Dr OLEG OLEYNIK
From 1984 to 1993 — Oleg Oleynik graduated from the Physics
and Technology Department (Phystech) of the Kharkov State University.
He obtained a Master’s degree in physics in physical metallurgy.
From 1993 to 1999 — was a senior engineer, scientific
assistant, postgraduate student, and a Soros postgraduate student.
In 1999 Oleg successfully graduated from the Phystech
postgraduate school, obtained his Ph.D.c specializing in experimental
nuclear physics and the physics of charged particle beams at the
Physics and Technology Department of the Kharkov State University.
This was followed by a preliminary defense of the thesis, with a positive review by D.S. V.T. Lazurik.
After 1999 Oleg left the Phystech department to pursue an independent career.
From 1999 to 2012 – Oleg Oleynik organized non-state research on
humanism on the Web, founded a School, a College, and a University with
academic degrees.
| 




