|
ligaspace метод параллакса
| |
| codegrinder | Дата: Четверг, 07.10.2010, 09:55 | Сообщение # 61 |
|
Сержант
Объединение: Пользователи
Сообщений: 31
Награды: 0
Репутация: 0
Статус: Offline
| Я пока не готов к анализу лунных фотографий, у меня нет точных параметров камеры, и т.д. Даже на нормальную ректификацию ушла куча времени, потому что трудно работать, а вечером переключаться на другую, совсем непростую работу. И даже когда буду готов, вы будете последним человеком, с которым я захочу говорить.
Пользуясь случаем уберу ту пургу которую вы нанесли про синтетические снимки. Математические точки нереальны точно так же как и синтетические сцены - у них нет размера, например; это абстракция. Чистая перспективная проекция, которая используется в компьютерных играх из-за её простоты - точно такая же абстракция, но именно этим она и удобна для анализа - нет дисторсии, можно шагнуть точно в сторону не сбив направление камеры, и т.д. Поэтому, вам придётся срочно взять назад вашу пургу. Но ведь вы этого не сделаете, просто нанесете ещё чего-нибудь, ведь ваша цель затормозить или остановить меня. О чем с вами после этого говорить?
|
| |
| |
| ligaspace | Дата: Четверг, 07.10.2010, 12:59 | Сообщение # 62 |
 Admin
Объединение: Администраторы
Сообщений: 185
Награды: 0
Репутация: 0
Статус: Offline
| Quote (codegrinder) И даже когда буду готов, вы будете последним человеком, с которым я захочу говорить.
Отлично! Quote (codegrinder) Пользуясь случаем уберу ту пургу которую вы нанесли про синтетические снимки. Математические точки нереальны точно так же как и синтетические сцены - у них нет размера, например; это абстракция. Чистая перспективная проекция, которая используется в компьютерных играх из-за её простоты - точно такая же абстракция, но именно этим она и удобна для анализа - нет дисторсии, можно шагнуть точно в сторону не сбив направление камеры, и т.д. Поэтому, вам придётся срочно взять назад вашу пургу. Но ведь вы этого не сделаете, просто нанесете ещё чего-нибудь, ведь ваша цель затормозить или остановить меня. О чем с вами после этого говорить?
Ок! Играем в блиц-шахматы "Наша логика". Мой первый ход:
Любой снимок имеет перспективу: параллельные продольные линии сходятся на бесконечности (у горизонта), параллельные верикальные линии сходятся на бесконечности (над головой в небе).
Пример, сходимость у горизонта ж/д путей.
Любой снимок способен передать удаленный горизонт, но не удаленную до бесконечности вертикаль. Да и все объекты съемки в реальности имеют конечную высоту. Это приводит к тому, что практически все вертикали (углы домов, столбы, заборы) сохраняют взаимную параллельность.  Пример параллельности вертикальных линий на снимках На компьютерной симуляции мы видим  Компьютерная симуляция - вертикали параллельных линий сходятся под полом. Вертикали предметов не параллельные и сходятся под полом. Это есть нарушение реальной картины снимков. Объявляю Вам шах!
|
| |
| |
| codegrinder | Дата: Четверг, 07.10.2010, 13:58 | Сообщение # 63 |
|
Сержант
Объединение: Пользователи
Сообщений: 31
Награды: 0
Репутация: 0
Статус: Offline
| Доигрались, объявите себе мат. Формулы проецирования для перспективной проекции: xs = f * x / z
ys = f * y / z Это значит, что если камера стоит не параллельно, скажем, к вертикальному столбу, а немного наклонена вниз, то в системе координат камеры верх столба будет иметь меньшую координату по z. А это значит, что при смещении в сторону они сместятся по разному, и даже если предмет на изначальном снимке был вертикальным, то всё равно станет наклонным. Наоборот тоже может быть. Угол наклона сохранится лишь в случае если оба конца имеют одну и ту же z-координату, т.к. в этом случае концы столба сместятся одинаково. xs1 = f * x / z
xs2 = f * (x+deltaX) / z
xs2-xs1 = f * deltaX / z При смещении x поменяется одинаково, а смещение двух точек с разными z получится разным. И завязывайте нести пургу. P.S. Ко всему прочему вы ещё и неправильно представляете что означает "сходится в бесконечности" в нашем случае. Если на фотографии с рельсами уходящими вдаль провести линии по рельсам, они тоже сойдутся и пересекутся, ибо на снимке - не параллельны. Бесконечность же, где они сходятся, находится в направлении куда они уходят, т.е. за пределами плоскости снимка. Точка пересечения проекций рельс на снимок может лежать прямо на снимке или быть совсем рядом.
Сообщение отредактировал codegrinder - Четверг, 07.10.2010, 15:06 |
| |
| |
| ligaspace | Дата: Четверг, 07.10.2010, 17:10 | Сообщение # 64 |
 Admin
Объединение: Администраторы
Сообщений: 185
Награды: 0
Репутация: 0
Статус: Offline
| Quote (codegrinder) Формулы проецирования для перспективной проекции: xs = f * x / z
ys = f * y / z Это значит, что если камера стоит не параллельно, скажем, к вертикальному столбу, а немного наклонена вниз, то в системе координат камеры верх столба будет иметь меньшую координату по z. А это значит, что при смещении в сторону они сместятся по разному, и даже если предмет на изначальном снимке был вертикальным, то всё равно станет наклонным. Наоборот тоже может быть. Угол наклона сохранится лишь в случае если оба конца имеют одну и ту же z-координату, т.к. в этом случае концы столба сместятся одинаково. xs1 = f * x / z
xs2 = f * (x+deltaX) / z
xs2-xs1 = f * deltaX / z При смещении x поменяется одинаково, а смещение двух точек с разными z получится разным.
Такой ответ ожидал.  Это была шахматная уловка, чтобы точно знать Ваш ответный ход. Прекрасно! Это была шахматная уловка, чтобы точно знать Ваш ответный ход. Прекрасно! Второй ход: Представьте, что Вы парите, найдите точку в пространстве для съемки камерой, чтобы получить подобные перспективные искажения на переднем крае и в глубине.
Такой точки вы не найдете. Она не существует! А если и существует, то вы увидите, что в реальности помещение сплющено и никаких десятков метров от одного края к другому нет. У Вас же наблюдатель находится практически на одной горизонтальной плоскости с другими предметами снимка. Он не смотрит буквально вниз. Он не парит над колоннами. Так ведь!.. Согласно методике стереоскопического дальномера с постоянной базой у Вас параллакс вертикальной колонны в основании и вершине составляет b-b' и b-b" (см. ниже анимацию). Или до основания метровой колонны 10 метров, а до её вершины 14 метров. Понимаете! Подобная несуразность касается любых других предметов данной компьютерной симуляции. 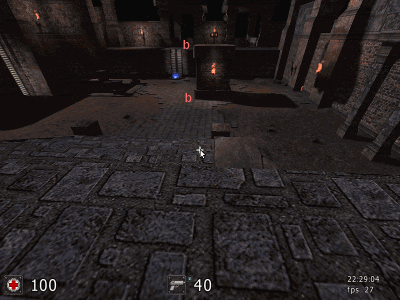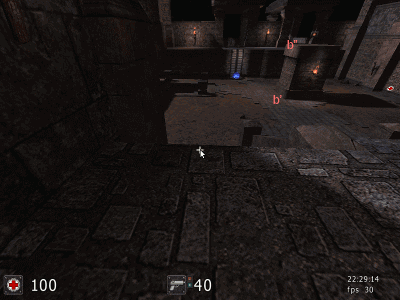 До основания вертикальной колонны 10 метров, а до вершины той же колонны 14 метров. Это несуразность для метровой высоты вертикальной колонны и суть искажений компьютерной симуляции. Другими словами: от вас до стоящего стула: до ножек 10 метров, а до его сидения 20 метров. Табурет Сальвадора Дали! Те же искажения для другой приведенной Вами компьютерной картинки: 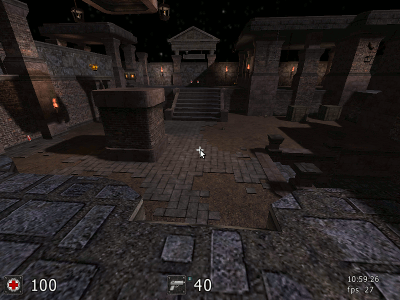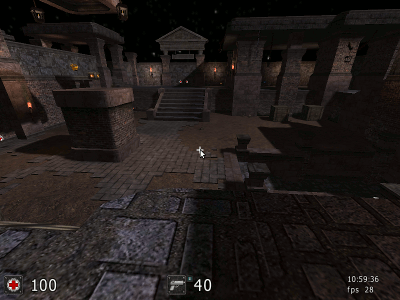 Другой пример компьютерной симуляции: нарушение перспективы и искажения взаимных расстояний Всё это несоответствие между расстояниями стереоскопического эффекта и искажения компьютерной симуляцией. Такие картинки возможны только в компьютерной симуляции! Объявляю Вам шах и мат!
|
| |
| |
| codegrinder | Дата: Четверг, 07.10.2010, 18:52 | Сообщение # 65 |
|
Сержант
Объединение: Пользователи
Сообщений: 31
Награды: 0
Репутация: 0
Статус: Offline
| Засчитайте себе второй мат. Расстояние не равно z-координате, а именно о ней говорит параллакс. Ко всему прочему, мне очень неловко указывать столь продвинутому фотограмметристу на то, что от точки съемки расстояние до вершины и до основания колонны действительно отличается (насколько именно надо посчитать, и не так как вы это делаете), это третий, видимо мат. Мне уже просто смешно, так что продолжайте, не стесняйтесь. Вы так классно обкладываете себя матами.  P.S. Думал вы хоть после этого остановитесь
Quote (codegrinder) Поэтому, вам придётся срочно взять назад вашу пургу. Но ведь вы этого не сделаете, просто нанесете ещё чего-нибудь
но видно, вас не волнует, что вас видно насквозь.
Сообщение отредактировал codegrinder - Четверг, 07.10.2010, 19:58 |
| |
| |
| ligaspace | Дата: Четверг, 07.10.2010, 22:33 | Сообщение # 66 |
 Admin
Объединение: Администраторы
Сообщений: 185
Награды: 0
Репутация: 0
Статус: Offline
| codegrinder, это эмоции на проигрыш. Quote (codegrinder) Формулы проецирования для перспективной проекции:
xs = f * x / z
ys = f * y / z
Это значит, что если камера стоит не параллельно, скажем, к вертикальному столбу, а немного наклонена вниз, то в системе координат камеры верх столба будет иметь меньшую координату по z. А это значит, что при смещении в сторону они сместятся по разному, и даже если предмет на изначальном снимке был вертикальным, то всё равно станет наклонным. Наоборот тоже может быть. Угол наклона сохранится лишь в случае если оба конца имеют одну и ту же z-координату, т.к. в этом случае концы столба сместятся одинаково.
xs1 = f * x / z
xs2 = f * (x+deltaX) / z
xs2-xs1 = f * deltaX / z
При смещении x поменяется одинаково, а смещение двух точек с разными z получится разным.
Это написано вами правильно. Возьмите несколько кубиков и погоняйте их проекции на плоскость. Когда будете иметь правильные представления, тогда переходите к алгоритму составления стереопар по снимкам.
|
| |
| |
| codegrinder | Дата: Четверг, 07.10.2010, 23:02 | Сообщение # 67 |
|
Сержант
Объединение: Пользователи
Сообщений: 31
Награды: 0
Репутация: 0
Статус: Offline
| Да вы что, давно так не веселился :). Погоняйте сами, когда разберетесь, пришлите открытку. А то мне страшно за математику как науку. Формулу расстояния s^2 = x^2+y^2+z^2 уже что, отменили? Или может, наблюдатель находится как раз напротив половины высоты столба? Я доходчиво объясняю? Вы переигрываете пытаясь показаться идиотом. Мы-то знаем, что вы просто гений, только маскируетесь.
Сообщение отредактировал codegrinder - Четверг, 07.10.2010, 23:03 |
| |
| |
| ligaspace | Дата: Пятница, 08.10.2010, 00:50 | Сообщение # 68 |
 Admin
Объединение: Администраторы
Сообщений: 185
Награды: 0
Репутация: 0
Статус: Offline
| Quote (codegrinder) Формулу расстояния s^2 = x^2+y^2+z^2 уже что, отменили?
Такой формулы расстояния для евклидового (нашего) пространства никогда не было!
Правильно: расстояние(x,y) = {суммаi (xi - yi)2 }1/2 для любого многомерного евклидового пространства. codegrinder, вы совсем запутались. Нарушаете нормы сетевого этикета. Короче, разбирайтесь и приводите себя в норму.
|
| |
| |
| ligaspace | Дата: Пятница, 08.10.2010, 11:20 | Сообщение # 69 |
 Admin
Объединение: Администраторы
Сообщений: 185
Награды: 0
Репутация: 0
Статус: Offline
| Вернемся к разлому Rima Hadley (смотри сообщение 60 - Разлом Rima Hadley) Длина не менее 135 км, ширина ~ 1,2 км и глубина ~ 370 м (от Грили (1971) указаны в Леверингтон Ф..  Ландшафт и маршруты Аполлон 15 с точки зрения художника для НАСА с обозначением станций 1-14 Рассмотрим снимки AS15-85-11423HR и AS15-85-11424HR со станции 2 с видом на разлом Rima Hadley:  Официальные AS15-85-11423HR и AS15-85-11424HR с сайта НАСА, станция 2 с видом на разлом Хадли. Горизонтальным стереоскопический эффект. После 1) использования только оптических преобразований: масштабирование, поворот, дисторсия, перспектива, сдвиг и смещения по х и у ко всему снимку в целом, 2) требования максимального вычитания удаленного ландшафта и 3) выделения горизонтального стереоскопического эффекта, получаем следующую стереопару  Стереопара снимков AS15-85-11423HR и AS15-85-11424HR с горизонтальным стереоскопическим эффектом после оптических преобразований Хорошо виден стереоскопический параллакс, по которому можно предварительно оценить расстояние до противоположного склона разлома Хэдли. Расстояние составляет не больше 50 метров. (Напомню, что по топографической карте должно быть не меньше 1 км). Удаленный ландшафт на стереопаре незначительно смещается. Хотя параллакс должен быть равен нулю, ибо по НАСА до этих гор около 20 км. Удаленный ландшафт на стереопаре можно привести в точности друг к другу. Для этого выходят за рамки оптических преобразований и производят цифровое искажения по элементам, а не в целом к снимку. Ниже приведен результат преобразования по элементам снимка.  Стереопара снимков AS15-85-11423HR и AS15-85-11424HR после оптических преобразований и цифрового искажения удаленного ландшафта. Указаны расстояния до элементов снимка, в метрах с погрешностью расстояний 3, 11, 20, 40 и 60 метров, соответственно, 1%, 2%, 15%, 30% и 45%.... Интересным объектом оказывается результат преобразования или сетка искажений удаленных объектов на снимке Аполлон 15. Сетка искажений имеет криволинейную поверхность и, соответствует, обратной проекции на плоскость круговой панорамы. Грубая оценка радиуса круговой панорамы 100-400 метров. Для большей точности оценки радиуса круговой панорамы необходима строить сетку искажений с большим разрешением. Масштабный стереоскопический эффект. Для AS15-85-11423HR и AS15-85-11424HR был так же выделен масштабный стереоскопический эффект, когда камера приближается к объекту съемки.  Стереопара снимков AS15-85-11423HR и AS15-85-11424HR с масштабным стереоскопическим эффектом после преобразований 1) использования оптических преобразований: масштабирование, поворот, дисторсия, перспектива, сдвиг и смещения по х и у ко всему снимку в целом, 2) цифровое искажение удаленного ландшафта, 3) требования максимального вычитания удаленного ландшафта, 4) выделения масштабного стереоскопического эффекта.. Указаны расстояния до элементов снимка, в метрах с погрешностью не более 60%. Хорошо виден масштабный стереоскопический параллакс, по которому оценено расстояние до противоположного склона разлома Хэдли. Расстояние составляет не больше 50 метров. Удаленный ландшафт снимков Аполлон 15. Ниже показана сетка цифрового искажения удаленного ландшафта снимков Аполлон 15.
 Сетка цифровых искажений удаленных объектов на снимке AS15-85-11424HR после оптических преобразований для приведения к AS15-85-11424HR. Сетка цифровых искажений удаленных объектов на снимке Аполлон 15 имеет криволинейную поверхность и, соответствует, симметричной проекции круговой панорамы на плоскость. 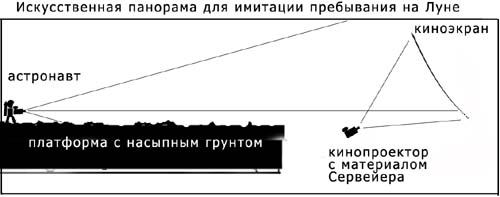 Логика и простота симуляции лунной панорамы миссии Аполлонов Оценка радиуса круговой панорамы даёт расстояние 70-150 метров. Предварительные выводы и заключение: смотри сообщение 74.
|
| |
| |
| Лунный_Гоблин | Дата: Пятница, 08.10.2010, 21:37 | Сообщение # 70 |
 Рядовой
Объединение: Пользователи
Сообщений: 9
Награды: 0
Репутация: 0
Статус: Offline
| Quote (ligaspace) Мы видим относительное горизонтальное смещение поверхности, обратное и вертикальное смещение на склоне «горы». Расстояние La до любого объекта A рассчитывается по формуле:
La =Lb x b / a
Где Lb – расстояние до объекта В, b – смещение объекта В, а – смещение объекта А. (Это принцип оптического дальномера, действия которого основаны на решении прямоугольного или равнобедренного треугольника по известной длине базы и измеренному противоположному углу).
Например, зная расстояние до ближайшего отпечатка бота "В" – 5 метров, измерив величину смещения бота "b" – 44 мм, и смещение любого другого объекта "a" на снимке, мы получаем расстояни Где в этой формуле учтены параметры камеры, ошибки измерения размеров и расстояние до "бесконечно" удаленных обьектов? "Метод параллакса" ligaspace субъективен, то есть при одинаковом наборе исходных фото, разные исполнители могут получить различные результаты из-за недостаточной формализации метода. Используется предположение о технике фальсификации:

(возможен логический порочный круг) Однако в фальсификации может использоваться другая техника, например Front Screen Projection:

http://ligaspace.my1.ru/forum/26-69-1#2290
Сообщение отредактировал Лунный_Гоблин - Суббота, 09.10.2010, 00:10 |
| |
| |
| ligaspace | Дата: Суббота, 09.10.2010, 01:06 | Сообщение # 71 |
 Admin
Объединение: Администраторы
Сообщений: 185
Награды: 0
Репутация: 0
Статус: Offline
| Лунный_Гоблин, хорошие вопросы. Интересное предположение об использовании зеркал. Спасибо! Quote (Лунный_Гоблин) Где в этой формуле учтены параметры камеры, ошибки измерения размеров и расстояние до "бесконечно" удаленных объектов?
Параметры камеры и расстояния до "бесконечно" удаленных объектов мы учитываем при сведении двух снимков в стереопару. Это задача многих неизвестных, имеем систему уравнений, но точек на снимке ещё больше. Сведение их содержат в себе дисторсию, фокусное расстояние, перспективу, смещение осей и прочее. Сведение снимков - есть математическое решение. Т.е., мы не считаем параллакс в пространстве, формула расчета которого очень сложная из-за тригонометрии, требует точных оптических данных и этим занимаются академические (военные) офисы, мы упрощаем задачу - выделяем в пространстве горизонтальный, вертикальный или масштабный параллакс. Какой-либо один! Выделение какого-либо параллакса (горизонтальный, вертикальный, масштабный) делает программный алгоритм Adobe Photoshop, используя законы тригонометрии. Это же делают другие программы работы с изображениями. В итоге, мы получаем смещения по стереопаре, которые подчиняются простому решению прямоугольного или равнобедренного треугольника по известной длине базы и измеренному противоположному углу. Такая формула приведена в статье и Вами указана. На остальные вопросы ответ после субботы! 
|
| |
| |
| codegrinder | Дата: Суббота, 09.10.2010, 10:37 | Сообщение # 72 |
|
Сержант
Объединение: Пользователи
Сообщений: 31
Награды: 0
Репутация: 0
Статус: Offline
| Нехорошо стирать сообщения, повторяю. Quote (ligaspace)
Такой формулы расстояния для евклидового (нашего) пространства никогда не было!
Правильно: расстояние(x,y) = {суммаi (xi - yi)2 }1/2 для любого многомерного евклидового пространства.
Поскольку одна из точек находится в начале координат, формула будет именно такой как я сказал. Так что идите разберитесь сами. Впрочем, чего это я, вы всё прекрасно понимаете, только придуриваетесь. Quote (ligaspace)
расстояние(x,y) = {суммаi (xi - yi)2 }1/2
Степени забыли.
Сообщение отредактировал codegrinder - Суббота, 09.10.2010, 10:38 |
| |
| |
| ligaspace | Дата: Суббота, 09.10.2010, 16:19 | Сообщение # 73 |
 Admin
Объединение: Администраторы
Сообщений: 185
Награды: 0
Репутация: 0
Статус: Offline
| Формула расстояния для евклиового пространства:
расстояние(x,y) = {суммаi (xi - yi)2 }1/2
это
расстояние(x,y) = {суммаi (xi - yi)2}1/2 Приведенной вами формулы расстояния: Формула расстояния s^2 = x^2+y^2+z^2 , нет. Есть s = (x^2+y^2+z^2)^1/2 или s = {x2 + у2 + z2}1/2 codegrinder, мне приходится вам напоминать школьный курс физики, объяснять очевидные вещи, которые понятны каждому, только не вам, говорить вам о правилах сетевого этикета, своих ошибок вы не признаете, упрямы, делаете голословные сообщения, глупыми сообщениями вы забираете у меня время, данную тему вы превращаете в балаган или разговор не о чём. Вы отдаете себе в этом отчёт?
Нет, тогда вам будет поставлен бан на неопределенное время.
|
| |
| |
| ligaspace | Дата: Суббота, 09.10.2010, 23:44 | Сообщение # 74 |
 Admin
Объединение: Администраторы
Сообщений: 185
Награды: 0
Репутация: 0
Статус: Offline
| Предварительные выводы и заключение по снимкам разлома Rima Hadley (см. сообщение 69). Можно с высокой вероятностью говорить о том, что удаленный ландшафт в миссии Аполлонов снят с киноэкрана. Об этом так же говорят другие исследования. 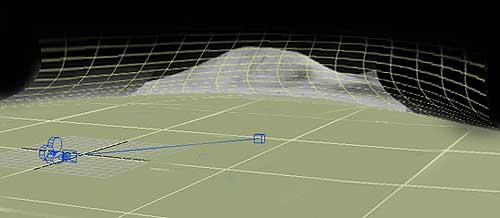 Логика и простота симуляции лунной панорамы миссии Аполлонов. Сеткой показан киноэкран, который опоясывает место симуляции миссии Аполлонов Это значит, что удаленный ландшафт ЛЮБЫХ стереопар пребывания американцев на Луне будет сводиться обратным преобразованием:
 Обратное преобразование для удаленных ландшафтов на снимках Аполлон говорит об искусственности лунных ландшафтов Проверкой данного предположения мы займемся на примере снимков AS15-85-11424HR и AS15-85-11449HR со станции 2 с видом на разлом Rima Hadley:  Официальные снимки AS15-85-11424HR и AS15-85-11449HR со станции 2 с видом на разлом Rima Hadley |
| |
| |
| ligaspace | Дата: Воскресенье, 10.10.2010, 13:05 | Сообщение # 75 |
 Admin
Объединение: Администраторы
Сообщений: 185
Награды: 0
Репутация: 0
Статус: Offline
| Quote (Лунный_Гоблин) "Метод параллакса" ligaspace субъективен, то есть при одинаковом наборе исходных фото, разные исполнители могут получить различные результаты из-за недостаточной формализации метода.
О субъективности не совсем так. Дело в том что сведение снимков в стереопару с требованием максимального вычитания удаленного ландшафта - это решении системы более миллиона уравнений (количество точек). Задача не простая, требует аккуратности и времени, а не шапкозакидательства. Решение сведения снимков приведено выше на примере снимков AS15-85-11423HR и AS15-85-11424HR. Ясно, что решение системы уравнений из более чем миллиона уравнений в рамках оптических преобразований и кругового экрана вокруг места съемки намного весомое доказательство, чем просто идеи. И попробуйте самостоятельно свести два снимка в стереопару. Вы поймете, что это не просто, потребует не 10 и не 60 минут, для первого опыта - несколько часов рабочего времени. По поводу формализации метода надо согласиться. Можно лучше и яснее его описать.
|
| |
| |
|





